Utilice el solucionador en Excel para encontrar la ruta más corta desde el nodo S al nodo T en una red no dirigida. Los puntos de una red se denominan nodos (S, A, B, C, D, E y T). Las líneas de una red se denominan arcos (SA, SB, SC, AC, etc.).
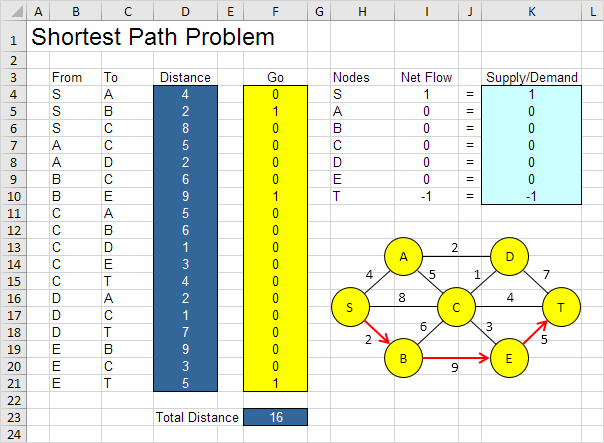
El modelo que vamos a resolver tiene el siguiente aspecto en Excel.
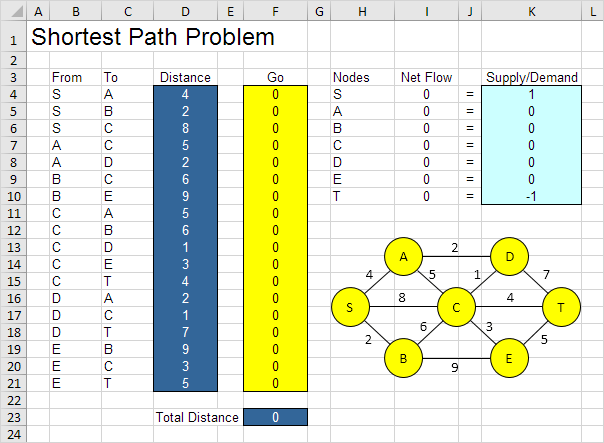
1. Para formular este problema del camino más corto , responda las siguientes tres preguntas.
una. ¿Cuáles son las decisiones a tomar? Para este problema, necesitamos Excel para averiguar si un arco está en la ruta más corta o no (Sí = 1, No = 0). Por ejemplo, si SB es parte de la ruta más corta, la celda F5 es igual a 1. Si no, la celda F5 es igual a 0.
B. ¿Cuáles son las limitaciones de estas decisiones? El flujo neto (flujo de salida - flujo de entrada) de cada nodo debe ser igual a la oferta / demanda. El nodo S solo debe tener un arco saliente (flujo neto = 1). El nodo T solo debe tener un arco entrante (flujo neto = -1). Todos los demás nodos deben tener un arco saliente y un arco entrante si el nodo está en la ruta más corta (flujo neto = 0) o no hay flujo (flujo neto = 0).
C. ¿Cuál es la medida general de desempeño para estas decisiones? La medida general del rendimiento es la distancia total del camino más corto, por lo que el objetivo es minimizar esta cantidad.
2. Para facilitar la comprensión del modelo, cree los siguientes rangos con nombre .
| Nombre de rango | Células |
|---|---|
| Desde | B4: B21 |
| Para | C4: C21 |
| Distancia | D4: D21 |
| Vamos | F4: F21 |
| NetFlow | I4: I10 |
| OfertaDemanda | K4: K10 |
| Distancia total | F23 |
3. Inserte las siguientes funciones.
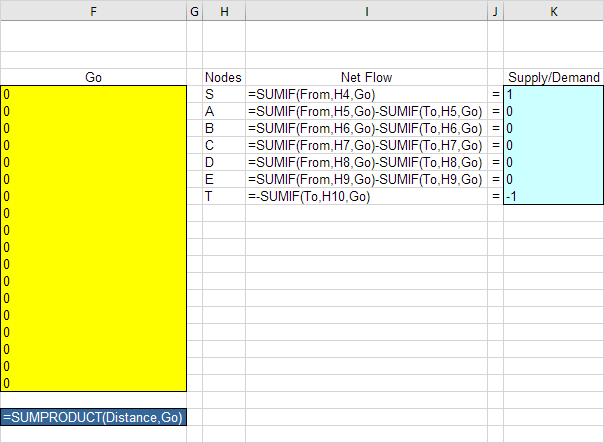
Explicación: Las funciones SUMIF calculan el flujo neto de cada nodo. Para el nodo S, la función SUMIF suma los valores de la columna Ir con una "S" en la columna Desde. Como resultado, solo la celda F4, F5 o F6 pueden ser 1 (un arco saliente). Para el nodo T, la función SUMIF suma los valores de la columna Ir con una "T" en la columna Hasta. Como resultado, solo las celdas F15, F18 o F21 pueden ser 1 (un arco entrante). Para todos los demás nodos, Excel busca en la columna Desde y Hasta. La distancia total es igual al sumproducto de Distancia e Ir.
Con esta formulación, resulta fácil analizar cualquier solución de prueba.
1. Por ejemplo, la ruta SBET tiene una distancia total de 16.
No es necesario utilizar prueba y error. A continuación, describiremos cómo se puede utilizar Excel Solver para encontrar rápidamente la solución óptima.
Para encontrar la solución óptima, ejecute los siguientes pasos.
1. En la pestaña Datos, en el grupo Analizar, haga clic en Solver.
Nota: ¿no puede encontrar el botón Solver? Haga clic aquí para cargar el complemento Solver .
Ingrese los parámetros del solucionador (siga leyendo). El resultado debe ser coherente con la imagen siguiente.
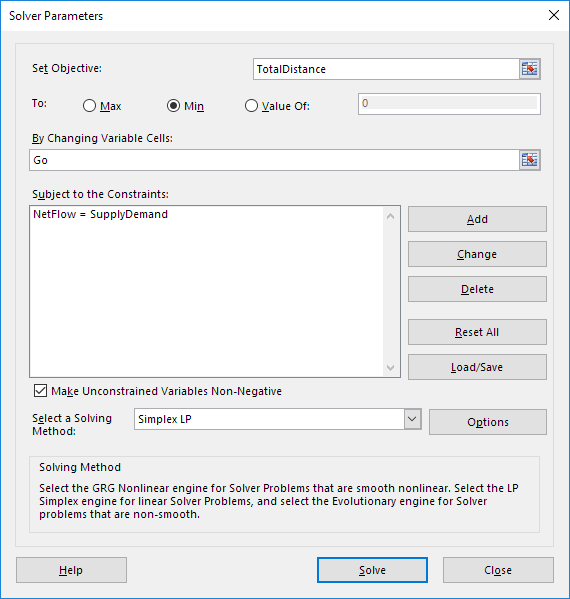
Tiene la opción de escribir los nombres de los rangos o hacer clic en las celdas de la hoja de cálculo.
2. Ingrese Distancia Total para el Objetivo.
3. Haga clic en Mín.
4. Ingrese Ir para cambiar las celdas variables.
5. Haga clic en Agregar para ingresar la siguiente restricción.
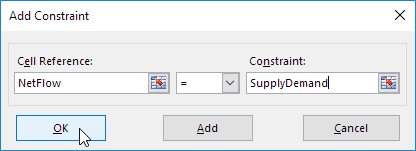
6. Marque 'Hacer que las variables no restringidas no sean negativas' y seleccione 'LP simplex'.
7. Por último, haga clic en Resolver.
Resultado:
La solución óptima:
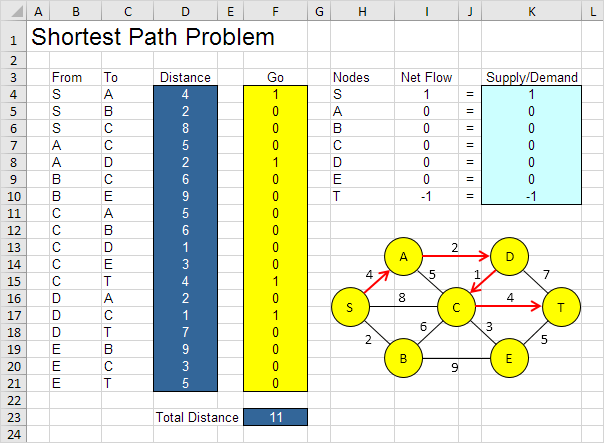
Conclusión: SADCT es el camino más corto con una distancia total de 11.
4/7 Completado! Obtenga más información sobre el solucionador>
Siguiente capítulo: Herramientas de análisis